19.（本小题满分12分）
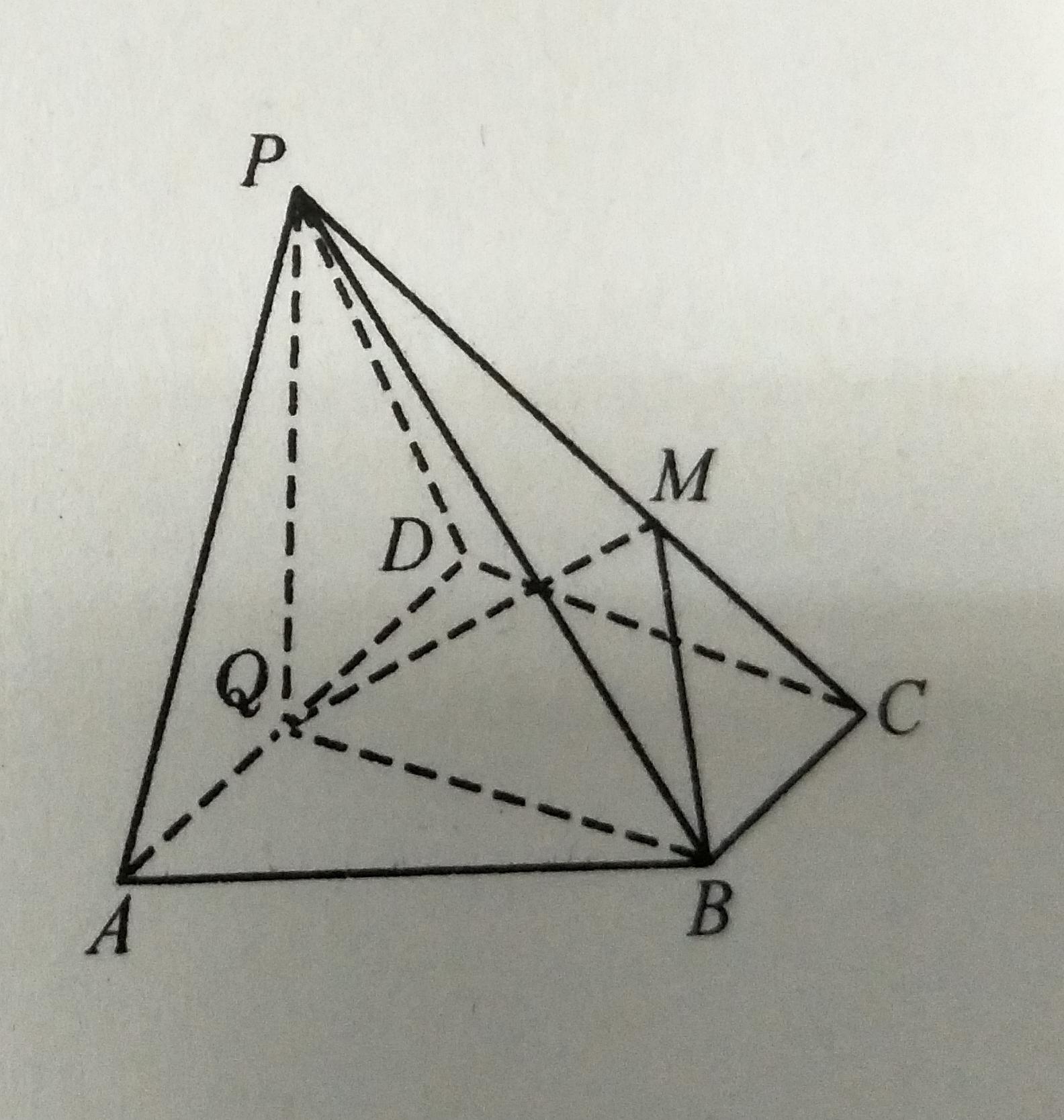
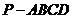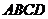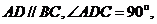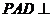如图，在四棱锥中，底面为直角梯形，平面底面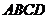，Q为AD的中点.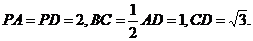
（1）求证：平面PQB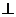平面PAD；
（2）在棱PC上是否存在一点M，使二面角M-BQ-C为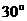？若存在，确定M的位置；若不存在，请说明理由.
考点说明：空间中的线面垂直关系；空间向量所成角的余弦值
提示性解答：（1）问中，易知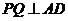（等腰三角形的性质）且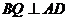（直角梯形的性质），注意证明过程中的逻辑；
（2）解决空间中关于二面角的余弦值的问题，通常情况下的方法依旧是建立适当的空间直角坐标系，通过空间向量间的关系来解答关于二面角的问题；本题中值得注意的是，点M在线段PC上，故须有一额外的限定条件，如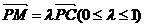，最终化为一个关于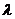的方程，如果关于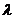的解存在，则存在对应的点M（具体解法见答案全解精析，此解答仅为编辑提示解题方法用，并不代表全解精析中所用解法）
另：《2017全国高考模拟试卷汇编38+2套》也即将上市，感谢您支持恩波图书！