题目

编辑解答
本题是一道典型的考查复数几何意义的问题;(1)问虽然也可以按照一般方法设z=a+bi去求解,但是计算量较大,不建议使用。
编辑解答:
(1)解法1(几何意义法) 由于|z+3|+|z-3|=10,易知点Z到点(3,0)和点(-3,0)的距离之和为10,考虑几何意义知Z的轨迹为以这两点为焦点,长轴长为10的椭圆;
易知椭圆的焦点在x轴上,a=5,c=3,从而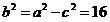 ,故所求点Z的轨迹方程为
,故所求点Z的轨迹方程为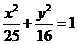 ,
,
根据椭圆的性质可知椭圆上的点到原点的距离最大为长轴长,最小为短轴长,故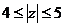 。
。
【解法2(一般方法) 设z=a+bi,则由条件得|a+3+bi|+|a-3+bi|=10,即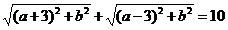 ,
,
两边平方,得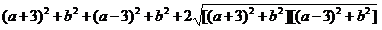 =100,整理,移项,得:
=100,整理,移项,得: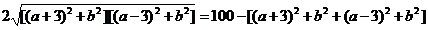 =
=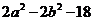
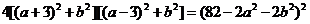 ,两边再平方,
,两边再平方,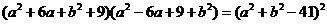 ,
,
逐步展开,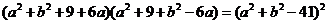 ,即
,即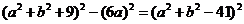 ,又即
,又即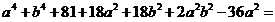 ,从而
,从而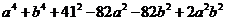 ,移项消元得
,移项消元得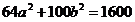 ,即
,即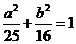 ,这是一个长轴长为10,焦距为6且焦点在x轴上的椭圆,下同解法1。
,这是一个长轴长为10,焦距为6且焦点在x轴上的椭圆,下同解法1。
注意:此方法计算量较大,不建议使用,单独列出为了方便比较。】
(2)|z+2|+|z-5-5i|的几何意义是,Z的轨迹((1)中所求得的椭圆)上的点到点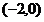 的距离与到点
的距离与到点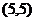 的距离之和;
的距离之和;
分析可知点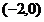 在椭圆内部,点
在椭圆内部,点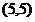 在椭圆外部,易知此两点所成的线段与椭圆有公共点,由“两点之间直线段最短”可知|z+2|+|z-5-5i|的最小值即为点
在椭圆外部,易知此两点所成的线段与椭圆有公共点,由“两点之间直线段最短”可知|z+2|+|z-5-5i|的最小值即为点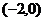 与点
与点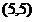 之间的距离,故|z+2|+|z-5-5i|
之间的距离,故|z+2|+|z-5-5i|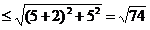 ,所求最小值为
,所求最小值为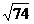 。
。

微信小程序
微信扫一扫体验

微信公众账号
微信扫一扫加关注
评论 返回
顶部

发表评论 取消回复