高考数学文科小题狂做·最基础篇(2016年4月 第3版)
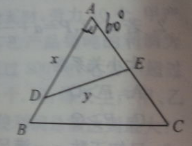
如图,江北水城湖畔有一块边长为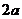 的等边三角形的草坪,在这块草坪内安装灌溉水管
的等边三角形的草坪,在这块草坪内安装灌溉水管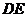 ,使
,使 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分,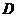 在
在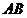 上,
上,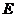 在
在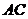 上。
上。
(1) 设
设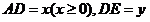 ,求
,求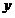 关于
关于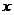 的函数关系式;
的函数关系式;
(2)为节约成本,应如何安装,才能使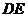 最短,最短是多少?
最短,最短是多少?
考点说明:解三角形;基本不等式的应用
提示性解答:
本题的解题关键在于“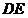 把△
把△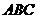 分成面积相等的两部分”;△
分成面积相等的两部分”;△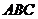 是边长为
是边长为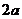 的等边三角形,面积易求,从而△
的等边三角形,面积易求,从而△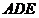 的面积也可以确定;
的面积也可以确定;
来思考求△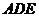 面积的方法吧:
面积的方法吧:
我们学习过的三角形面积公式有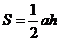 和
和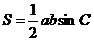 两种,一种是需要知道一边上的高,另一个使用的两边长和它们的夹角(然而实质上两者是一致的,因为
两种,一种是需要知道一边上的高,另一个使用的两边长和它们的夹角(然而实质上两者是一致的,因为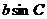 就是
就是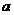 边上的高)
边上的高)
在△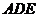 中,确定的角有一个,从而其面积可以使用这个角来求出,而
中,确定的角有一个,从而其面积可以使用这个角来求出,而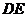 边的长度可以由余弦定理求出,以上是本题的整体解题思路。
边的长度可以由余弦定理求出,以上是本题的整体解题思路。
大体过程如下:
△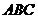 的面积为
的面积为 ,从而△
,从而△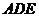 的面积应为
的面积应为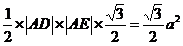 ,得到
,得到 ;
;
在△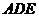 中,由余弦定理可得
中,由余弦定理可得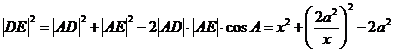 ,从而
,从而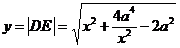 ,注意x的取值范围,显然
,注意x的取值范围,显然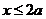 且
且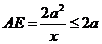 ,故
,故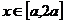
观察易知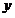 的解析式的根号中,含有x的两项的积有定值,故可以使用基本不等式求其最值,注意等号成立的条件即可
的解析式的根号中,含有x的两项的积有定值,故可以使用基本不等式求其最值,注意等号成立的条件即可

微信小程序
微信扫一扫体验

微信公众账号
微信扫一扫加关注
评论 返回
顶部

发表评论 取消回复