浙江学考 A01-5 Q24
已知椭圆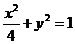 ,
,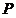 是椭圆的上顶点,过点
是椭圆的上顶点,过点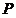 作斜率为
作斜率为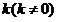 的直线
的直线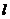 交椭圆于另一点
交椭圆于另一点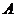 ,设点
,设点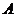 关于原点的对称点为
关于原点的对称点为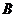 (图略).
(图略).
(1)求△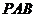 面积的最大值;
面积的最大值;
(2)设线段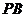 的中垂线与
的中垂线与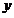 轴交于点
轴交于点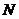 ,若点
,若点 在椭圆内部,求斜率
在椭圆内部,求斜率 的取值范围.
的取值范围.
考点说明:椭圆;直线与圆锥曲线的综合问题
提示性解答:
首先由椭圆方程易知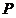 点坐标,而后可直接设出
点坐标,而后可直接设出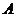 点坐标从而得到
点坐标从而得到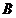 点坐标;也可直接由斜率写出直线的点斜式方程;(1)问整体有两种做法,一种是用直线方程与弦长公式、点到直线距离去求
点坐标;也可直接由斜率写出直线的点斜式方程;(1)问整体有两种做法,一种是用直线方程与弦长公式、点到直线距离去求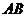 的长及
的长及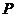 到
到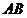 的距离(高);也可以利用
的距离(高);也可以利用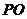 为公共底,将△
为公共底,将△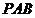 分为△
分为△ 和△
和△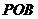 两个部分,利用椭圆上的点的横坐标的有界性解答;整体来说设直线方程的方法计算量很大,不建议使用;
两个部分,利用椭圆上的点的横坐标的有界性解答;整体来说设直线方程的方法计算量很大,不建议使用;
(2)问中由于涉及到中垂线,要注意 的中点、
的中点、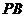 的斜率,从而可以得到所求中垂线的方程,其与
的斜率,从而可以得到所求中垂线的方程,其与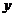 轴交于点
轴交于点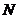 ,易求出点
,易求出点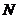 的纵坐标,而
的纵坐标,而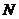 在椭圆内,注意纵坐标的取值范围便可求出斜率
在椭圆内,注意纵坐标的取值范围便可求出斜率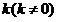 的取值范围,剩余就是计算问题了。
的取值范围,剩余就是计算问题了。

微信小程序
微信扫一扫体验

微信公众账号
微信扫一扫加关注
评论 返回
顶部

发表评论 取消回复